Arrays

Static data structures that store elements of the same type in contiguous memory locations. An array can be accessed based on its index, and can be made up of of a single line (a one-dimensional array) or a multi-dimensional array in the form of a matrix.

There are two types of arrays: Static arrays and Dynamic arrays.

Arrays are commonly zero-indexed and the index itself represents positions in contiguous memory locations. For example, suppose we have the following array: numbers = [1, 10, 2, 20].

At index 0, meaning numbers[0] the value of the array is 1. At index 3, the last item, the value is 20. This maps to a location in memory in the following way:

address	index	value
0x00500	n/a	data
0x00504	0	1
0x00508	1	10
0x0050C	2	2
0x00510	3	20
0x00514	n/a	data

Note

The index itself is not physically present in memory.

Note

Because numbers are often stored in 4 byte sequences, the actual memory register will actually be continous ⇒ 0x00500 0x00501 0x00502 0x0503, rather than jumping for each value as shown in the table.

The array begins at memory address 0x00504, and after that it continues until and including 0x00510. Around it can be other data but the values in the array itself are contiguous.

When we access an array, the 0-index position points at the location where the array begins. In the above image, stock_prices[0] points to 0x00500. If we want to access the element at index 2 - that is, stock_prices[2] - the computer will use the following:

stock_prices[i] -> 0x00500 + i * sizeof(integer)

In this case, the size of each integer is 4 bytes, giving us 0x00500 + 2 * 4 = 8 = 0x00508

Important

The simple function above to find the element at any given index has a Big-O notation value of O(1) → it takes a single operation to find the requested location, regardless of the size of the array

On the other hand, looking for a specific index location based on a value often requires us to potentially iterate over all n elements of the array (assuming the value we are seeking is the last one). As a result, the lookup by value cost is O(n)

Big-O values

Find the value of an element based on its index location has a constant cost of O(1), since it utilizes the formula above to arrive at the value.

On the other hand, looking for the index of an element, printing all the elements, or adding/deleting elements to the array has a value of O(n):

• Looking for an index requires, at worst, to traverse all values in a list while keeping track of their index until we find the one we are looking for.
• Adding an element requires shifting the entire array, one by one, in order to insert the element into the array. The same is true for deleting elements, since all elements have to be “unshifted”.

Dynamic arrays

If we increase the size of an array (for example, by inserting new items into it), the memory locations will have to change. For example:

computers = ["trantor", "helicon", "synnax"]
computers.insert(2, "anacreon")
 
-> ["trantor", "helicon", "anacreon", "synnax"]

This will cause each element after index 2 to be shifted up in memory locations to make space for the new element. Note that this requires either a new memory block that is large enough or that there is no data surrounding the memory block holding the array.

If we attempt to add an element beyond the initial capacity of a dynamic array, the program will now use 3 times the memory space of the initial array size. This is because, following the image above, the program will request an additional block of memory with twice as much capacity (a capacity of 20). This is known as geometric progression, where in each jump in requested capacity size will increase geometrically (i.e. if we request the addition of the 31st item, we will use 90 blocks of memory)

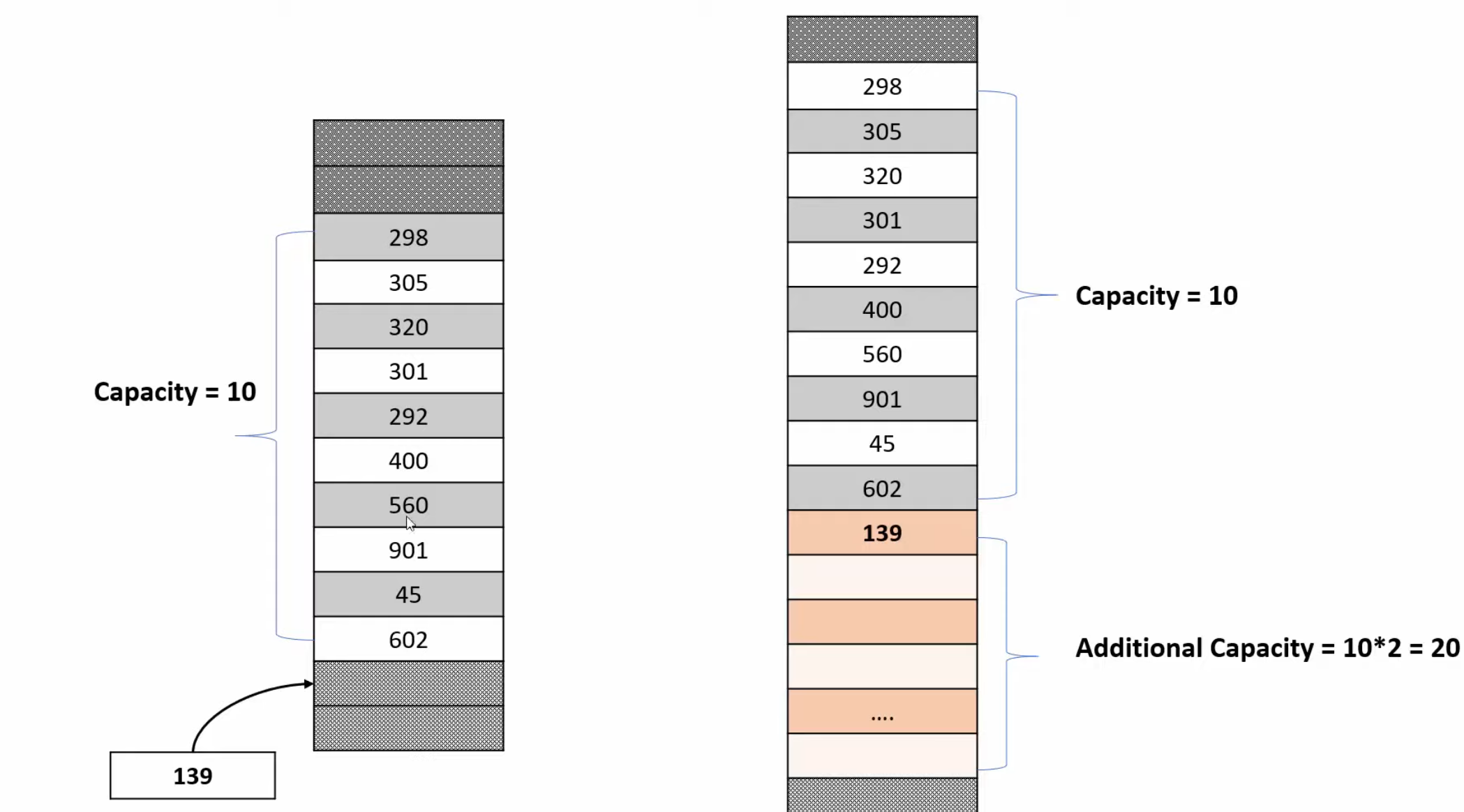
Static arrays

This is as opposed to static arrays, as seen in languages like C or Java, wherein we must declare the size of the array on initialization:

int[] stockPrices = new int[5]

Using JS arrays

let fruits = ["apple", "orange", "banana"];

To access each element in the array, we can use zero-based index notation:

console.log(fruits[0])

We can change the element at any given position by indexing into that position and assigning a value:

let computers = ["trantor", "synnax", "anacreon"];
computers[0] = "helicon";
computers[3] = "luna"

We can “push” elements to the end of the array, or, inversely, “pop” them out of the array:

let computers = ["trantor", "synnax", "anacreon"];
computers.push("helicon")
-> ["trantor", "synnax", "anacreon", "helicon"]
 
computers.pop();
-> ["trantor", "synnax", "anacreon"]

To add elements to the beginning we can “unshift” the array, or we can “shift” the array to remove the item (think of it as shifting the beginning of the memory block):

computers.unshift("luna")
-> ["luna", "trantor", "synnax", "anacreon"]
computers.shift();
-> ["trantor", "synnax", "anacreon"]

The length of an array can be accessed as follows :

numOfComputers = computers.length
-> 3

If we want to find the index of a specific element, assuming there is a match, we use “indexOf” (note that if we search for an element that doesn’t exist “indexOf” will return -1):

let index = fruits.indexOf("synnax")
-> 1

To loop over the array we can do the following:

let computers = ["trantor", "synnax", "anacreon", "helicon"]
 
for (let i = 0; i < computers.length; i++) {
	console.log(computers[i])
}
 
 
// To loop backwards we can reverse the conditional
// Note the length -1 due to zero-based index
for (let i = computers.length -1 ; i >= 0; i--) {
	console.log(computers[i])
}
 
// We can also use an "of" loop to make this shorter:
for (let computer of computers) {
	console.log(computer)
}

Sorting arrays

To sort an array we can use the sort() method:

let computers = ["trantor", "synnax", "anacreon", "helicon"]
computers.sort();
computers.sort().reverse();

Note

The sort method sorts the array in place