Proposition
A linked list exists to solve certain issues with Arrays, in particular that of memory allocation and retrieval. Recall that an array requires contiguous memory allocation; as a result, indexing into any element of an array has a low cost - a constant time of O(1). However, arrays are limited in that they are either static - meaning that the memory allocation is pre-defined and set - or dynamic, which allows them to grow or shrink.
The issue with the latter is that adding an element to an array requires a large amount of memory, with geometric growth - going beyond the last block of a 10-element array requires, if momentarily, space for 30 elements → 10 for the original array, 10 to copy it, and 10 more as expansion room.
Additionally, even without the issues of memory overflow, an array has a cost of O(n) when adding or removing elements to/from it - for example, an array of a million items will have a cost of at least a million operations.
A linked list does not occupy contigous space in memory. Each node in a linked list contains the address of the next item - think of it as a distributed array. This means that, after finding a specific location for insertion, all we have to do is add the value we want and then direct the new node pointer to the value of the old one.
Linked Lists
Unlike arrays, linked lists store data in different areas of memory, each linked by a pointer. The structure of each element will be the bytes allocated to the stored value, plus a pointer to a different memory location for the next element:
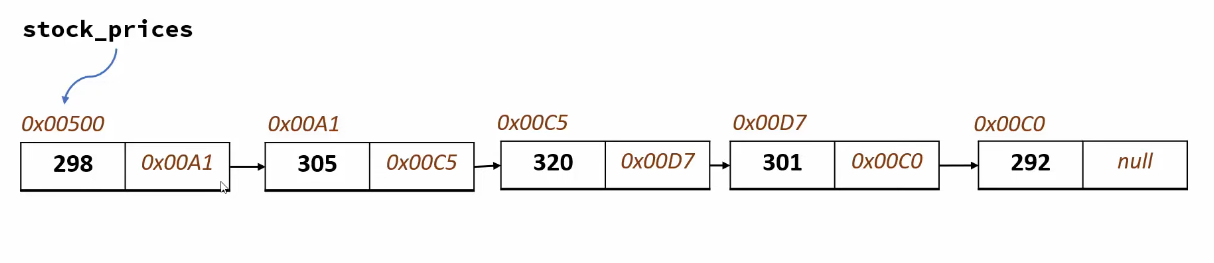
This allows us to very easily add new elements to the list without having the overhead of transferring the entire array to a new memory location:
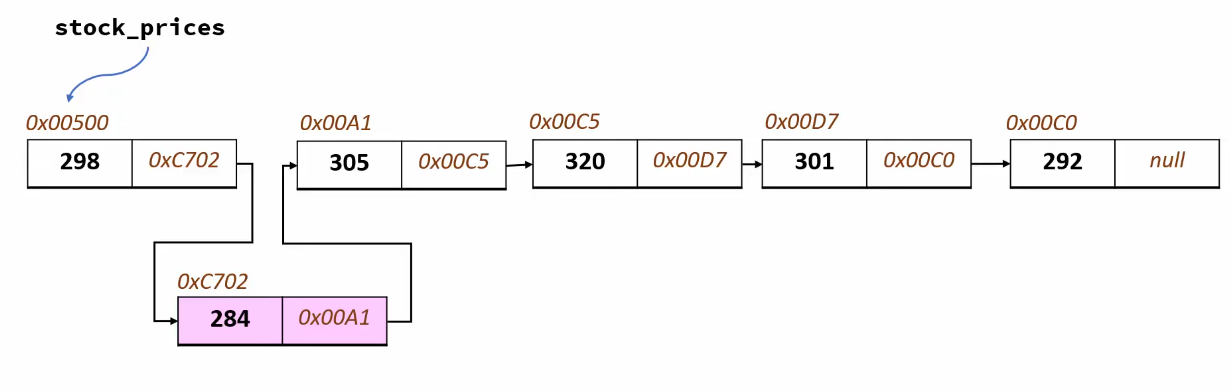
To indicate that a linked list has finished we simply place a null value as the reference item of the last element.
Double Linked List
A double linked list is a flavour of regular linked lists. They different simply in that they contain three elements per node: a pointer to the previous node, the element itself, and a pointer to the next node:
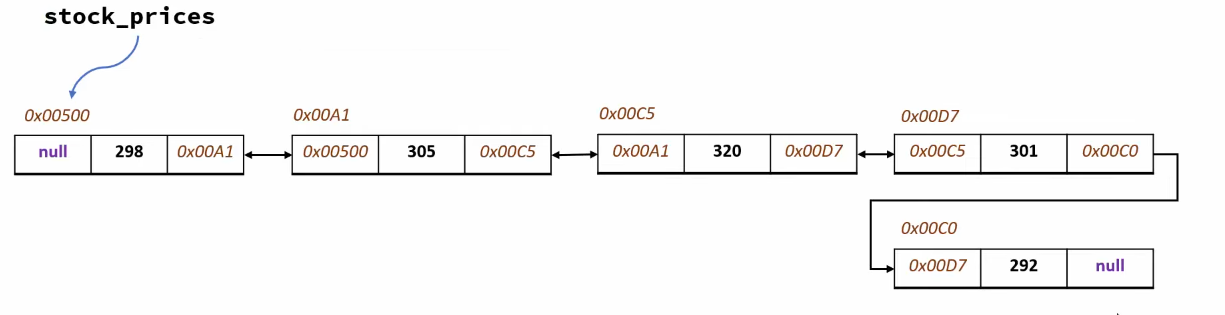
This allows for easily backwards traversal.
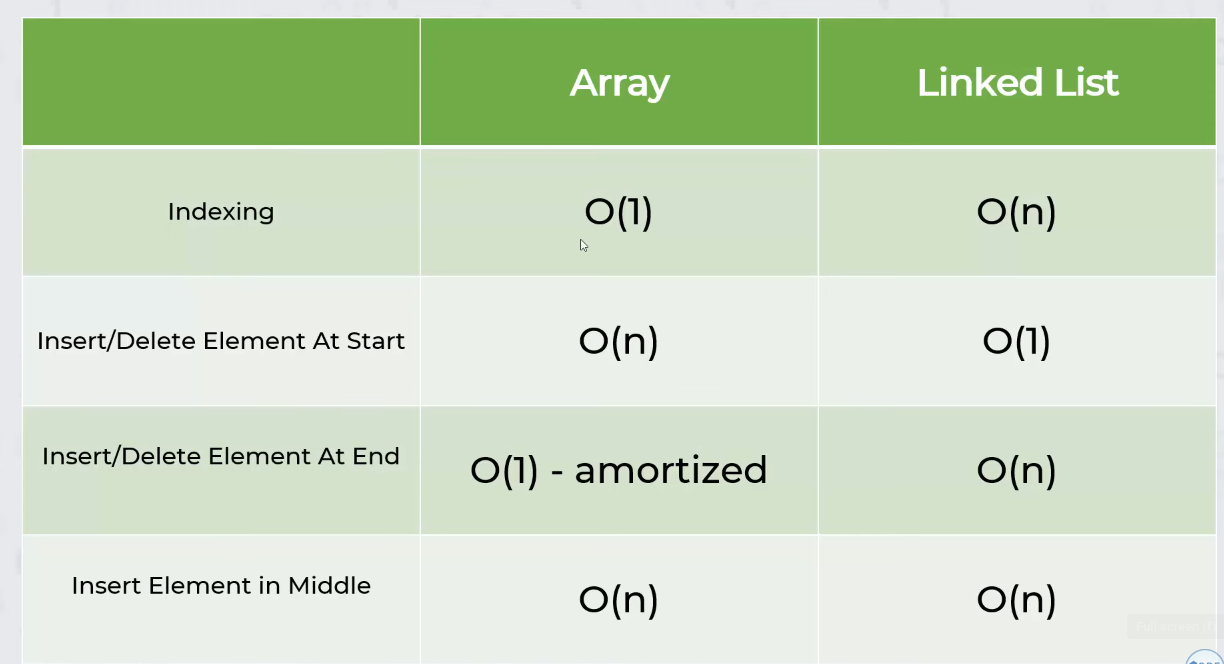
Big-O values
The structure of a linked list means that inserting or deleting an element at the beginning of the list will have a cost of O(1). The worst case scenario is inserting or deleting at the end of the list (or in the middle), where we must traverse the entire linked list to manipulate the last element, resulting in a cost of O(n).
Likewise, traversing a linked list and accessing the elements of a linked list by value is O(n), much like in an array. Note too that if you know the index of an item, an array is far more efficient than the linked-list, since it does not require traversing through the list and as a result has a cost of O(1) instead of O(n)
Note
The Big-O advantages of a linked-list over arrays in terms of insertions and deletions isn’t great. The true benefit is not having to pre-allocate memory space and the simplicity of the insertion/deletion operation.