Arbitrary Arity Tree

Let’s imagine we have to represent a file-system structure in code. That is to say, we want to have a data structure that represents a folder that has subfolders, that themselves may or may not have subfolders and files. The design of this structure must be arbitrary, as we don’t know beforehand how many files and folders will be present in the system.

When thinking of this structure, we can recognize that it is a tree with various relevant elements:

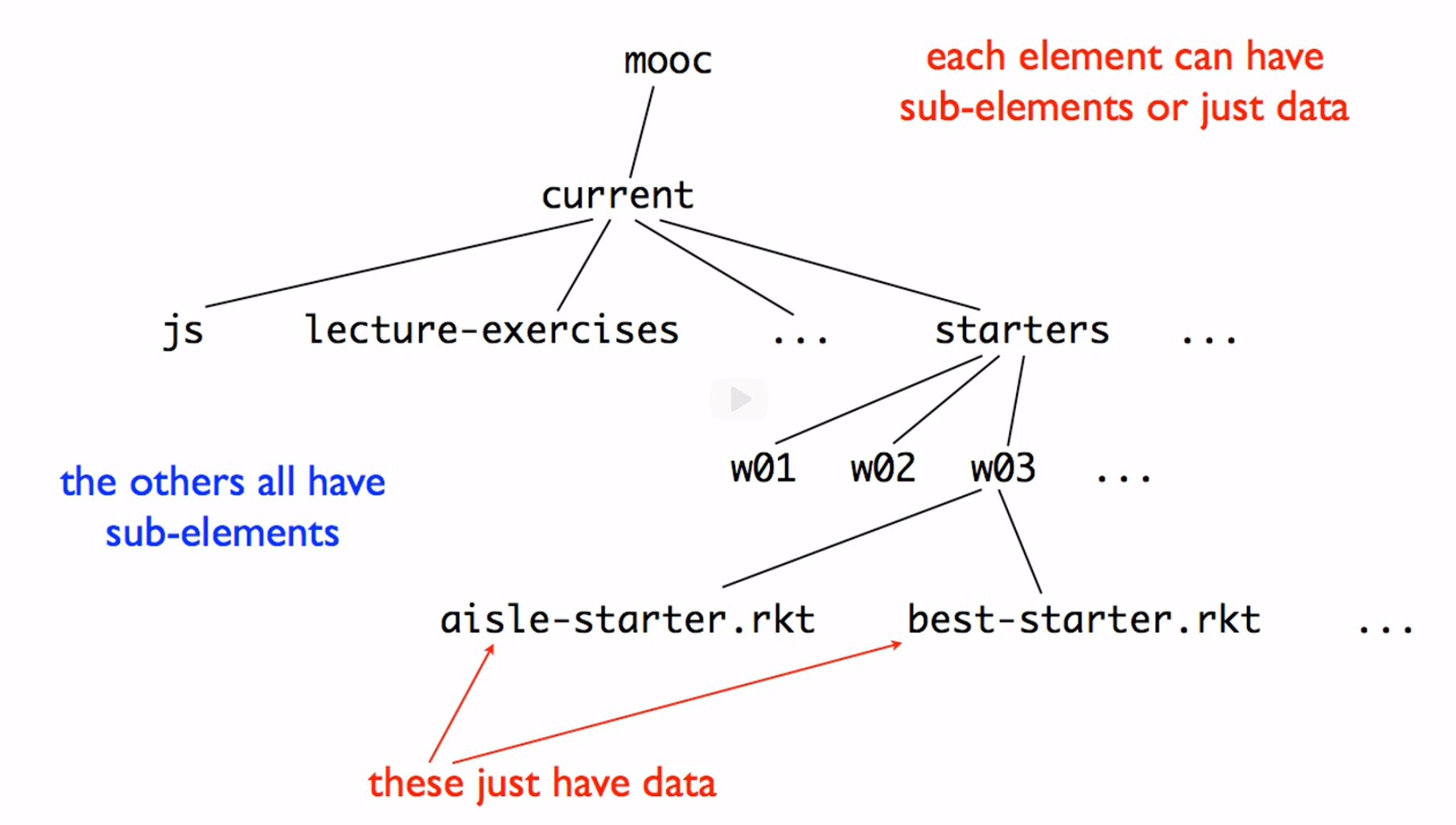
This type of data is said to have arbitrary arity because, unlike lists, the content may be arbitrarily deep and/or arbitrarily wide: each node may have an arbitrary number of nodes and subnodes.

As a result, we need to cycles in the type reference graph.

In order to make the arbitrary arity tree work, we need to have some manner of self referential information to allows to create sub-elements that are arbitrarily long.

Importantly, if we are constructing a list of elements to represent the folder/sub-folder structure, we should note that the structure definition also refers to the list itself. In other words, we have a cyclic reference cycle (or mutual reference in HtDD terms):

As a result, we have a mutual reference cycle between ListOfElement and elt as well as a self-reference cycle within ListOfElement.

When designing functions that operate on mutual references, we will always be creating at least two functions at once.

Example

(require 2htdp/image)
 
;; fs-starter.rkt (type comments and examples)
 
;; Data definitions:
 
(define-struct elt (name data subs))
;; Element is (make-elt String Integer ListOfElement)
;; interp. An element in the file system, with name, and EITHER data or subs.
;;         If data is 0, then subs is considered to be list of sub elements.
;;         If data is not 0, then subs is ignored.
 
;; ListOfElement is one of:
;;  - empty
;;  - (cons Element ListOfElement)
;; interp. A list of file system Elements
 
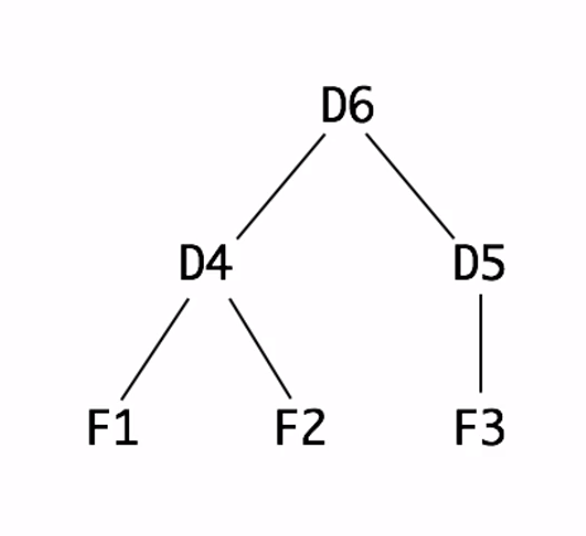
(define F1 (make-elt "F1" 1 empty))
(define F2 (make-elt "F2" 2 empty))
(define F3 (make-elt "F3" 3 empty))
(define D4 (make-elt "D4" 0 (list F1 F2)))
(define D5 (make-elt "D5" 0 (list F3)))
(define D6 (make-elt "D6" 0 (list D4 D5)))
 
(define (fn-for-element e)
(... (elt-name e)                  ;String
	  (elt-data e)                 ;Integer
	  (fn-for-loe (elt-subs e))))  ;ListOfElement
 
(define (fn-for-loe loe)
	(cond [(empty? loe) (...)]
			[else
			 (... (fn-for-element (first loe))
				  (fn-for-loe (rest loe)))]))
 
;; Functions:
 
; *Design a function that consumes Element and produces the sum of all the file data in the tree*
 
;; Element -> Integer
;; ListOfElement -> Integer
; produce sum of all data in element (and its subs)
(check-expect (sum-data--element F1) 1)
(check-expect (sum-data--loe empty)  0)
(check-expect (sum-data--element D5) 3)
(check-expect (sum-data--element D4) (+ 1 2))
(check-expect (sum-data--element D6) (+ 1 2 3))
 
 
;(define (sum-data--element e) 0)
;(define (sum-data--loe loe)   0)
 
 
(define (sum-data--element e)
(if (zero? (elt-data e))
	(sum-data--loe (elt-subs e))
	(elt-data e))) 
 
 
(define (sum-data--loe loe)
	(cond [(empty? loe) 0]
			[else
			 (+ (sum-data--element (first loe))
				(sum-data--loe (rest loe)))]))
 

This definition creates a structure elt that contains either files of subelements (files or subfolders, for example). The examples suggest this structure by using integers to refer to the content of said files, or 0 to suggest that there are no files and instead subfolders. The structure of the examples looks as follows: