Graphs

In arbitrary arity trees data is represented in a parent-child relationship. That is, supposing we have A, we can represent a tree with arrows like so:

A -> B
A -> D

The nature of the relationship here is one sided - one can only go from A to B or from A to D, but not the other way around. In Zork, for example, we can image these as rooms with one-way exits.

Graphs, however, increase the complexity of the data because they have connections that are cyclical (although acyclic graphs exist), and each of which can have zero or more arrows leading into a single node.

For example, a graph might have the following pattern: A -> B -> C -> A. Additionally, note that unlike the arity trees, we can have several paths leading into a single node - just as in this case both B and D lead to E.

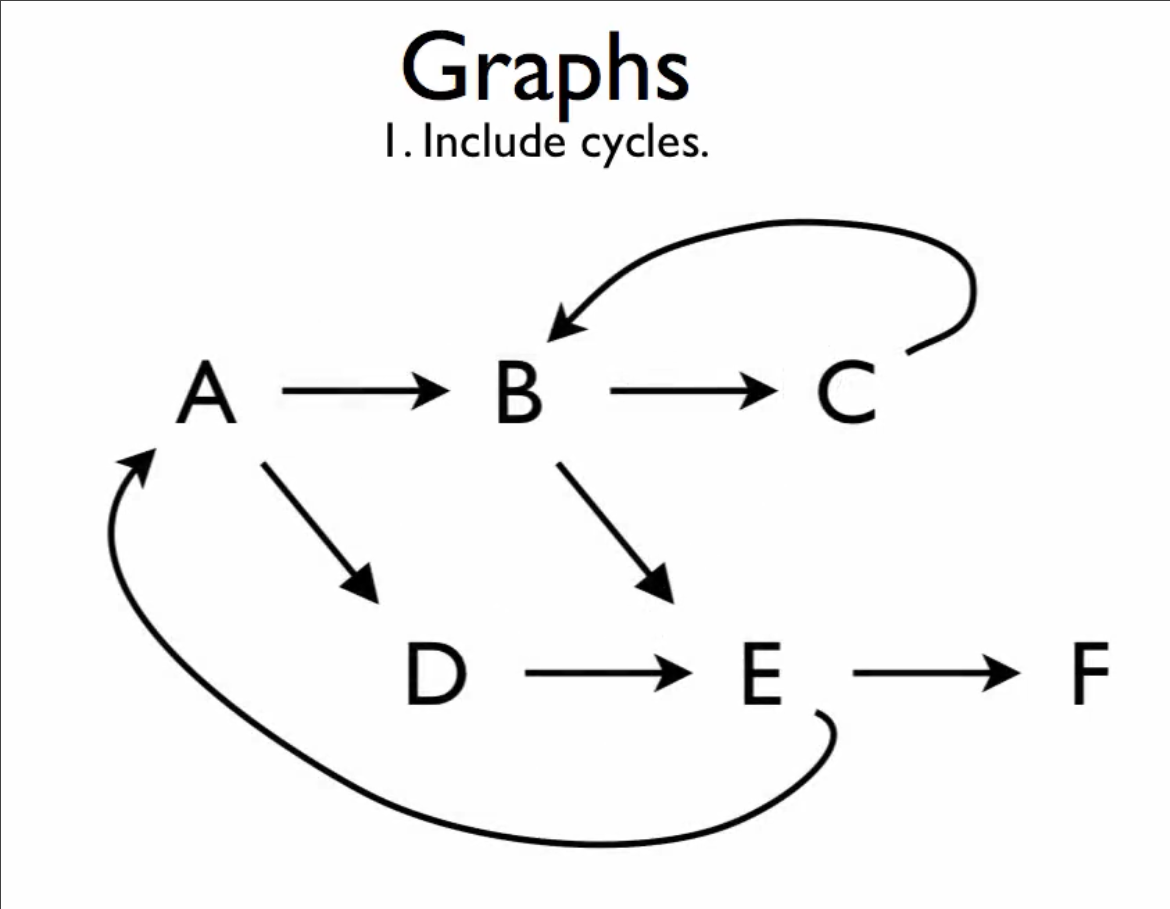
Defining graphs

Suppose want to design graph definitions to represent a series of rooms in a Zork-like game:

• A → B
• A → B → A
• A → B → C → A
• The image above

We can begin by creating a structure definition:

(define-struct room (name exits))
;; Room is (make-room String (listof Room))
;; interp. the room's name, and a list of rooms that the exits lead to
 
; A -> B
(define H1 (make-room "A" (list (make-room "B" empty))))

The first example is straightforward, since it is a unidirectional, acyclic graph. However, the second example becomes more complicated, since room B contains A, which is where we defined the room structure. Unlike a tree, there is no clear hierarchical structure where a parent contains the children but the children don’t contain the parent. Thus:

; using Racket ASL
(define H2
  (shared ((-0- (make-room "A" (list (make-room "B" (list -0-))))))
  -0-))
 
(define H3
  (shared ((-0- (make-room "A"
                           (list (make-room "B"
                                            (list (make-room "C"
                                                             (list -0-))))))))
    -0-))

Here, the -0- is like a promise. The -0- is a name for the result of the make-room expression for A. It allows us to refer to the this room inside the expression that generates the room itself.

Another way to read this is that -0- is the special promise name for the values that start at the first -0- and ends right before the second -0-. Note, too, that our definition of H2, then, is the result of the shared expression.

Note that as the graphs begin to get larger, we can use an alternative syntax:

(define H3
  (shared ((-A- (make-room "A" (list -B-)))
           (-B- (make-room "B" (list -C-)))
           (-C- (make-room "C" (list -A-))))
    -A-))

In either definition, calling H3 will still be shown by Racket as:

(shared ((-0- (make-room "A" (list (make-room "B" (list (make-room "C" (list -0-)))))))) -0-)

With this in mind, coding the structure of the image above with several cycles and paths becomes trivial:

(define H4
  (shared ((-A- (make-room "A" (list -B- -D-)))
           (-B- (make-room "B" (list -C- -E-)))
           (-C- (make-room "C" (list -B-)))
           (-D- (make-room "D" (list -E-)))
           (-E- (make-room "E" (list -A- -F-)))
           (-F- (make-room "F" empty)))
    -A-))

And it’s representation when called:

(shared ((-0- (make-room "A" (list -3- (make-room "D" (list -10-))))) (-10- (make-room "E" (list -0- (make-room "F" '())))) (-3- (make-room "B" (list (make-room "C" (list -3-)) -10-))))
  -0-)

Although difficult to read, the complexity comes from the nature of graphs and cyclical structures and not so much from the code itself represented in textual form.

Templating graphs

In a way, templates for graphs are a form of structural recursion, closely related to an arbitrary arity tree. In fact, one might start by modelling the required template with pseudocode:

1. Needs structural recursion
2. Because it’s like arity tree, encapsulate with local
3. Use a worklist accumulator to ensure we traverse all rooms
4. Context-preserving accumulator to mark rooms already visited (since graph is cyclical)

(define (fn-for-house r0)
 ;; todo is (listof Room) ; a worklist accumulator
 ;; visited is (listof String) ; a context preserving accumulator, names of rooms already visited
 (local [(define (fn-for-room r todo visited)
           (if (member (room-name r) visited)
               (fn-for-lor todo visited)
               (fn-for-lor (append (room-exits r) todo)
                           (cons (room-name r) visited))))
         (define (fn-for-lor todo visited)
           (cond [(empty? todo) (...)]
                 [else
                  (fn-for-room (first todo)
                               (rest todo)
                               visited)]))]
   (fn-for-room r0 empty empty)))

Note how this is simply a blend of various previously existing templates. Additionally, when we are trying to operate on a graph we can make whatever adjustments are required to produce the final result.