Binary Search Trees
A binary search tree is a method to find information in O(log n) time. It consumes a sorted list and then simply begins to split the list in the middle at each step. By doing so, a binary search tree is able to eliminate half the information in one go, thus making it much less painful to search for an answer.
The rules for a BST to work are as follows:
- a base case where the solution is found
- a sorted list of items
- a split down the middle each time, generating new sub-trees
Data definition
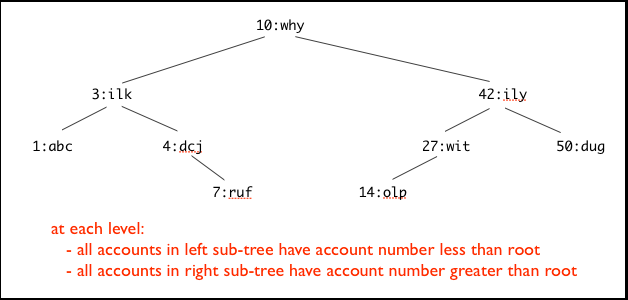
When looking at the BST, note that we have 4 values that naturally occur together: each node is composed of a key, a value, as well as a left-subtree and a right-subtree. Each of these sub-trees is also arbitrarily sized.
As a result, we need to design a compound data definition with two self-reference cycles:
;; Data definition
;; ===================
(define-struct node (key val l r))
;; BST is one of:
;; - false
;; - (make-node Integer String BST BST)
;; interp. false means no BST, or empty BST
;; key is the node key
;; val is the node val
;; l and r are left and right subtrees
;;INVARIANT: for a given node:
;; key is > all keys in left child
;; key is < all keys in right child
;; the same key never appears twice in the tree
(define BST0 false)
(define BST1 (make-node 1 "abc" false false))
(define BST4 (make-node 4 "dcj" false (make-node 7 "ruf" false false)))
(define BST3 (make-node 3 "ilk" BST1 BST4))
(define BST42
(make-node 42 "ily"
(make-node 27 "wit" (make-node 14 "olp" false false) false)
(make-node 50 "dug" false false)))
(define BST10
(make-node 10 "why" BST3 BST42))
(define (fn-for-bst t)
(cond [(false? t) (...)]
[else
(... (node-key t) ; Integer
(node-val t) ; String
(fn-for-bst (node-l t)) ; BST
(fn-for-bst (node-r t)))])) ; BST
;; Template rules used:
;; - one of: 2 cases
;; - atomic distinct: false
;; - compound: (make-node Integer String BST BST)
;; -self-reference: (node-l t) has type BST
;; Functions
;; ===================
;; BST Natural -> String or False
;; Try to find node with given key; if found, produce value, else produce false
(check-expect (lookup-key BST0 99) false)
(check-expect (lookup-key BST1 1) "abc")
(check-expect (lookup-key BST1 99) false)
(check-expect (lookup-key BST1 0) false)
(check-expect (lookup-key BST10 1) "abc") ; L L
(check-expect (lookup-key BST10 4) "dcj") ; L R
(check-expect (lookup-key BST10 27) "wit") ; R L
(check-expect (lookup-key BST10 50) "dug") ; R R
#;
(define (lookup-key t k) " ")
; template from BST with additional atomic parameter k
(define (lookup-key t k)
(cond [(false? t) false]
[else
(cond [(= k (node-key t)) (node-val t)]
[(< k (node-key t))
(lookup-key (node-l t) k)]
[(> k (node-key t))
(lookup-key (node-r t) k)])])) Example
Suppose we have a list of size n , where each element in the list is in the form Natural:String. If we were to search of a particular string given the corresponding natural, a solution would be to design a recursive function that starts at the beginning of the list and runs through it until the required value is found.
(list 1:abc 4:dcj 3:ilk 7:ruf 14:olp 10:why 50:dug 27:wit 42:ily ... n:string)However, notice that we might become concerned about the time required to complete such a function. For example, if we are finding an entry for 1, the searching requires looking at 1 account; a search for 4 requires looking at 2 accounts, etc. In other words, a search for n will take O(n) operations, which may be far too time consuming as the list continues to grow.
Note that on average the search operation described would take O(n/2) given a basic search distribution.
Sorting the existing list, while cumbersome, seems like a decent solution; it suggests that we can find numbers based on their size. However, if using the same algorithm as above we are still required to access random elements of the list starting at the beginning, leading to the same O(n) value.
On the other hand, if we sort the list and then begin searching in the middle, we can discard half the list, since we’ll know whether the number we want is higher or lower. We can then do this recursively, which allows us to find our answer in O(log n).
The effect of this method is to give us an “invariant” rule; that is, a rule that is true over the whole tree (in other words, it doesn’t vary):
- at each level:
- all numbers in left sub-tree are less than the root
- all numbers in right sub-tree are higher than the root