Accumulators
- Context Preserving Accumulators (preserve context lost in natural recursion)
- Result So Far Accumulators (help achieve tail recursion by eliminating pending operations)
- Worklist Accumulators (help achieve tail recursion by eliminating need to retain future recursive calls in pending operations)
Templating
HtDF Recipe
- Signature, purpose, stub
- Define examples and unit tests
- Template and inventory:
- Templates as usual, then
- wrap templated function with outer function of the same name, changing outer param name
- Add trampoline calling inner function with outer parameter name
- Add new parameter to inner function (the accumulator) after all
... - In calls to inner function specify type, invariant, and examples of accumulator
- Code function body
- Test and debug
Templating example
Steps to generating accumulator templates:
- Structural recursion template
- Wrapping in outer function, local, and trampoline
- Adding additional parameters
 We start with a standard structural recursion template:
We start with a standard structural recursion template:
(define (skip1 lox)
(cond [(empty? lox) (...)]
[else
(... (first lox)
(rest lox))]))We then wrap this templated function with an outer function of the same name, along with a local and a trampoline which calls the outer function with the outer parameter. The argument to the outer function should be given a different name:
(define (skip1 lox0)
(local [(define (skip1 lox)
(cond [(empty? lox) (...)]
[else
(... (first lox)
(rest lox))]))]
(skip1 lox0))) We then add a new parameter to the inner function, and pass it to every .... We must also include it in any call to the inner function. In this case, we used the parameter name acc. We must also add an additional argument to the trampoline call:
(define (skip1 lox0)
(local [(define (skip1 lox acc)
(cond [(empty? lox) (... acc)]
[else
(... acc
(first lox)
(skip1 (rest lox)
(... acc)))]))]
(skip1 lox0 ...))) Finally, we create space to define the type, invariant, and examples of the accumulator:
(Note: the accumulator invariant simply means something that’s always true about the accumulator, even if the actual value of the accumulator changes)
(define (skip1 lox0)
;; acc:
(local [(define (skip1 lox acc)
(cond [(empty? lox) (... acc)]
[else
(... acc
(first lox)
(skip1 (rest lox)
(... acc)))]))]
(skip1 lox0 ...))) Context Preserving Accumulators
This type of accumulator preserves context that would otherwise be lost through structural recursion.
For example, assume we have the following:
(define LON1 (list 1 2 3 4 5 6))If we want to design a function that skips every second number, called skip1, we can use the list template to create the following:
(define (skip1 lox)
(cond [(empty? lox) empty]
[else
(if (odd? POSITION?)
(cons (first lox)
(skip1 (rest lox)))
(skip1 (rest lox)))]))The issue here is that the (odd? POSITION) question is lost to the context of list functions, given that we use (first lox) and (rest lox). At every recursive call, we “forget” what is the current position we are operating on.
What we do now is to follow the accumulator templating steps and define the type of accumulator we want to use. In this case, we want the accumulator to represent the position of every item in the original list.
(define (skip1 lox0)
;; acc: Natural; 1-based position of (first lox) in lox0
...This comment serves as a purpose for the accumulator, so now we have to create examples. For those, work out the progression of calls to the inner function:
(define (skip1 lox0)
;; acc: Natural; 1-based position of (first lox) in lox0
;; (skip1 (list "a" "b" "c") 1)
;; (skip1 (list "b" "c") 2)
;; (skip1 (list "c") 3)
(local [(define (skip1 lox acc)
(cond [(empty? lox) empty]
[else
(if (odd? acc)
(cons (first lox)
(skip1 (rest lox)
(add1 acc)))
(skip1 (rest lox)
(add1 acc)))]))]
(skip1 lox0 1))) Note how, because this accumulator just has to count upwards, we were able to simply ask (odd? acc). Additionally, for every recursive call inside the if clause we used add1 acc to simply make it count one up.
Finally, in the trampoline we initialised the accumulator with a starting value (1, in this case, since we decided to use 1-based positions).
Result So Far Accumulators
Making a function tail recursive
- Template according to accumulator recipe
- Delete part of template wrapping around recursive call
- Move computation sthat would have been around recursive call into the accumulator argument position
Detailed example
For efficient computing we need to formulate recursive functions with the recursive calls placed in the tail position. To do so, we can make use of accumulators.
To generate a tail recursive function, we can start with a normal accumulator template:
(define (sum lon0)
;; acc:
(local [(define (sum lon acc)
(cond [(empty? lon) (... acc)]
[else
(... acc
(first lon)
(sum (rest lon)
(... acc)))]))]
(sum lon0 ...))) However, we have to make a change to ensure the recursive call to sum is in tail position. In other words, sum has to be the outermost call of the else clause.
In other words, the call to (+ (first lon)) needs to be moved into the accumulator position.
(define (sum lon0)
;; acc: Number; the sum of the elements in lon0 seen so far
;; (sum (list 2 4 5))
;; (sum (list 2 4 5) 0)
;; (sum (list 4 5) 2)
;; (sum (list 5) 6)
;; (sum (list ) 11) ; the answer needs to be here
(local [(define (sum lon acc)
(cond [(empty? lon) (... acc)]
[else
;(... acc
; (first lon)
(sum (rest lon)
(... acc))]))]
(sum lon0 ...))) We can see that the accumulator here is going to be increasing in value through each call.
With this structure in place, we can then add the required values to finish the computation without creating a long list of pending operations. From the accumulator example, we can see that once the list is empty we should return the value of acc. We can also see that in the recursive call, we must add (first lon) to the current value of acc. Finally, the initial value of acc must be 0. Thus:
(define (sum lon0)
;; acc: Number; the sum of the elements in lon0 seen so far
;; (sum (list 2 4 5))
;; (sum (list 2 4 5) 0)
;; (sum (list 4 5) 2)
;; (sum (list 5) 6)
;; (sum (list ) 11) ; the answer needs to be here
(local [(define (sum lon acc)
(cond [(empty? lon) acc]
[else
;(... acc
; (first lon)
(sum (rest lon)
(+ acc (first lon)))]))]
(sum lon0 0))) The issue with recursion
Consider a simple function that consumes a list and adds every element in that list (much in the way that foldr does).
(define (sum lon)
(cond [(empty? lon) 0]
[else
(+ (first lon)
(sum (rest lon)))]))If we call this function with (sum (list 1 2 3 4 5)), as the function traverses through its recursive structure we will end up with the following step:
(+ 1 (+ 2 (+ 3 (+ 4 (+ 5 0)))))Consider, then, that as the list of numbers to sum grows longer, so does this list of “pending” computation. Thus, given a list of 1 million numbers, there will be 1 million + operations waiting to occur.
The issue is that the context of the pending computation in store in the stack, which is an expensive and limited part of memory. As a result, we want to minimize its use.
Tail position
The reason the list gets built up is because the recursive call with the + operation is in what is known as the tail position:
(+ (first lon)
(sum (rest lon)))This is because the entire expression is evaluated as the result of +. Thus, we can consider than the call to the function sum, once valuated, simply equates to +.
To generalize, we can say that whenever an expression is in a position where its result is the result of the enclosing function, the expression is in tail position.
Note, however that neither (first lon) nor (sum (rest lon)) are in tail position. This is because both expressions are passed on to the + primitive - the sum call becomes an integer before being passed onto +.
Because (sum (rest lon)) is recursive call that is not in tail position, its structure causes the operation build up of pending operations.
Worklist Accumulators
Given an arbitrary arity tree, we can use worklist accumulators to traverse through the tree in a more efficient manner. For example, if we have to simply enumerate every node in a tree, we could use tail recursion to improve the efficiency of our code. However, by simply using tail recursion each juncture node would be accessed twice as we move up and down the tree.
The solution is to use a worklist accumulator, which will allow us to either traverse the tree in the vertical first or in the horizontal by directly accessing the next relevant node instead of backtracking.
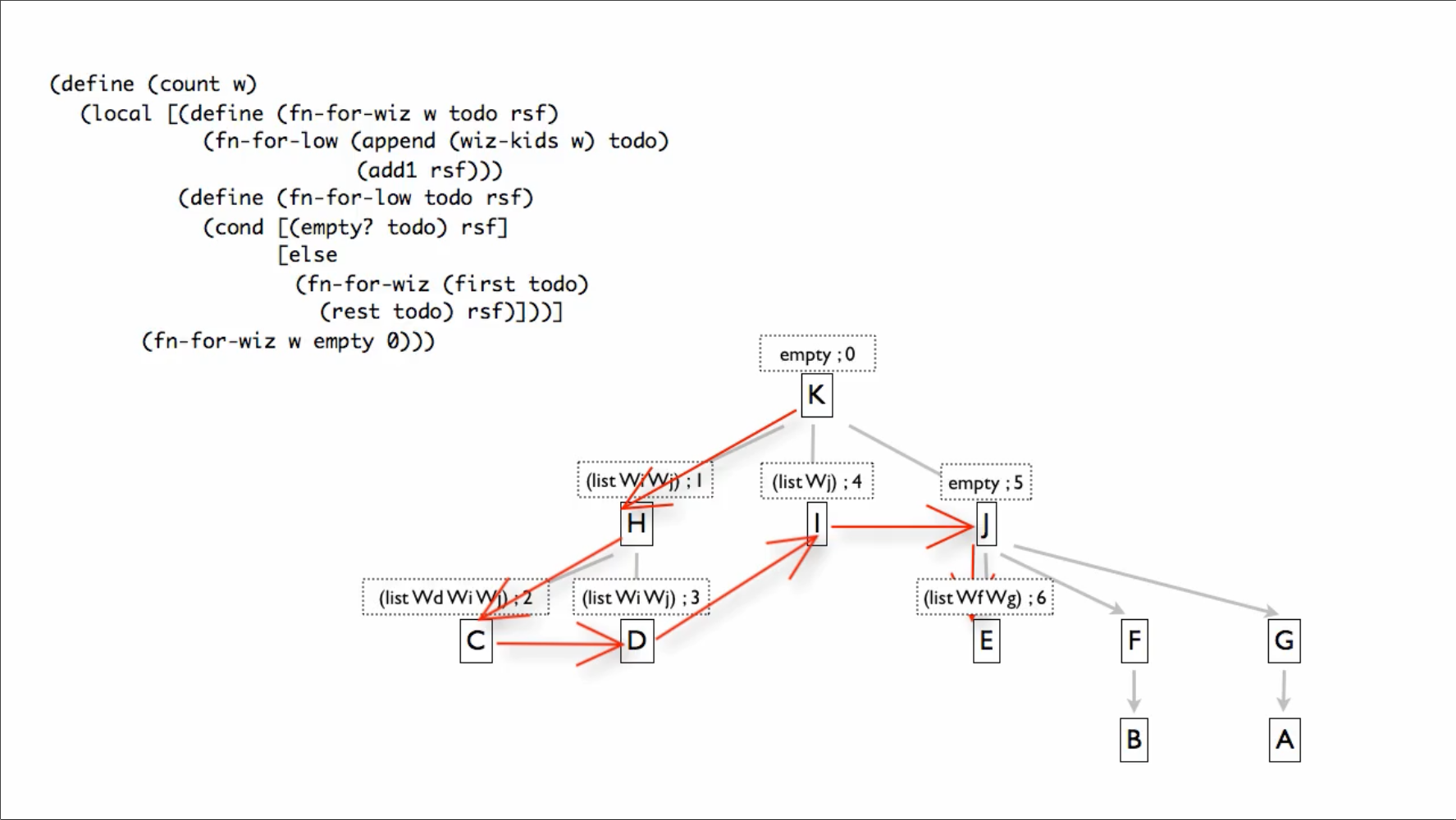
Worked example
Suppose we are to design a tail recursive function that consumes wizard and produces the number of wizards in that tree, including the root.
(define-struct wizard (name house children))
;; Wizard is (make-wizard String String ListOfWizard)
;; interp. a wizard is a person with name, a house, and children
;; House is:
;; - G for Gryffindor
;; - S for Slytherin
;; - R for Ravenclaw
;; - H for Hufflepuff
(define Wa (make-wizard "A" "S" empty))
(define Wb (make-wizard "B" "G" empty))
(define Wc (make-wizard "C" "R" empty))
(define Wd (make-wizard "D" "H" empty))
(define We (make-wizard "E" "R" empty))
(define Wf (make-wizard "F" "R" (list Wb)))
(define Wg (make-wizard "G" "S" (list Wa)))
(define Wh (make-wizard "H" "S" (list Wc Wd)))
(define Wi (make-wizard "I" "H" empty))
(define Wj (make-wizard "J" "R" (list We Wf Wg)))
(define Wk (make-wizard "K" "G" (list Wh Wi Wj)))
#;
(define (fn-for-wizard w)
(local [(define (fn-for-wizard w)
(... (wizard-name w)
(wizard-house w)
(fn-for-low (wizard-children w))))
(define (fn-for-low low)
(cond [(empty? low) (...)]
[else
(... (fn-for-wizard (first low))
(fn-for-low (rest low)))]))]
(fn-for-wizard w)))With this information, we can simply follow the accumulator template to arrive at this function design:
(define (count-wizards w)
;; acc Natural; the number of wizards in the tree so far
;; (count-wizards Wh)
;; (fn-for-wizard Wh 0) 1)
;; (fn-for-wizard Wc 1) 2)
;; (fn-for-wizard Wd 2) 3)
(local [(define (fn-for-wizard w acc)
(fn-for-low (wizard-children w)
(+ 1 acc)))
(define (fn-for-low low acc)
(cond [(empty? low) acc]
[else
(+ (fn-for-low (rest low) acc)
(fn-for-wizard (first low) acc))]))]
(fn-for-wizard w 0)))There two issues at this point. The first one is that the recursive calls in the second local function are not in tail position. The second issue is that because the tree is traversed up and down each time, the value of the accumulator is double counting several nodes.
To make the function tail recursive, then, we would have to effectively remove the + primitive and the call to fn-for-low:
(local [(define (fn-for-wizard w acc)
(fn-for-low (wizard-children w)
(+ 1 acc)))
(define (fn-for-low low acc)
(cond [(empty? low) acc]
[else
;; (+
;; (fn-for-low (rest low) acc)
(fn-for-wizard (first low) acc))]))]
(fn-for-wizard w 0)))Of course, at this point the function is no longer recursive. The solution is to add another accumulator to keep track of which nodes we still have to work through, for example by calling (fn-for-wizard (first low) (rest low) acc) with the added (rest low) parameter.
(local [(define (fn-for-wizard w acc)
(fn-for-low (wizard-children w)
(+ 1 acc)))
(define (fn-for-low low acc)
(cond [(empty? low) acc]
[else
;; (+
;; (fn-for-low (rest low) acc)
(fn-for-wizard (first low) (rest low) acc))]))]
(fn-for-wizard w 0)))We can then begin by adjusting fn-for-wizard by adding a “todo” parameter:
(local [(define (fn-for-wizard w todo acc) ; todo is (listof Wizard) ; wizards remaining to see
(fn-for-low (wizard-children w)
(+ 1 acc)))
(define (fn-for-low low acc)
(cond [(empty? low) acc]
[else
(fn-for-wizard (first low) (rest low) acc)]))]
(fn-for-wizard w 0)))Here, todo is a list of wizards we are yet to visit, while acc is the number of wizards we have already seen. The trick is then to ensure that fn-for-wizard tells fn-for-low about the todo parameter. In other words, we have to ensure that fn-for-low has access to the current wizard as well as the rest of the wizards in its recursive function call. If we simply append todo, we are telling the function that create a worklist of the existing to-do items and to add the children of the current wizard to that list.
(local [(define (fn-for-wizard w todo acc)
(fn-for-low (append (wizard-children w) todo)
(+ 1 acc)))
(define (fn-for-low todo acc)
(cond [(empty? todo) acc]
[else
(fn-for-wizard (first todo) (rest todo) acc)]))]
(fn-for-wizard w 0)))Here we added the todo param to fn-for-wizard and modified the call to fn-for-low to append both lists. For clarity, the parameters in the second function were renamed from acc to todo.
The end result is as follows:
(define (count-wizards w)
;; acc Natural; the number of wizards in the tree so far
;; todo is (listof Wizard) ; wizards remaining to see
;; (count-wizards Wh)
;; (fn-for-wizard Wh 0) 1)
;; (fn-for-wizard Wc 1) 2)
;; (fn-for-wizard Wd 2) 3)
(local [(define (fn-for-wizard w todo acc)
(fn-for-low (append (wizard-children w) todo)
(+ 1 acc)))
(define (fn-for-low todo acc)
(cond [(empty? todo) acc]
[else
(fn-for-wizard (first todo) (rest todo) acc)]))]
(fn-for-wizard w empty 0)))